The main focus of our space science group is ionospheric and magnetospheric physics. We investigate ionized gas in the planetary environments in the Solar System by means of theory, simulation and data analysis.

Aurorae (northern and southern lights) are among the most visible space physics phenomena. They have been observed on many planets of the solar system, like Jupiter for example. The conditions in the near-Earth space environment are commonly called the space weather. They include the changes in the magnetic fields (geomagnetic storms, ionospheric disturbances etc.) and the influence of energetic particles from the Sun (flares and coronal mass ejections). All these phenomena have direct or indirect influence on our lives (by damages to satellites, for example, or a power grid failure).

For further information on space physics and space weather we recommend the following websites:

Selected research results:

Sun’s Long-Term Variation

Because satellite-based radiometers have revealed continuous changes in the total solar irradiance and its spectral distribution since 1978

[e.g., Willson and Mordvinov, 2003], the constancy of the Sun is not assumed anymore. Understanding the variability of the Sun has important implications for both terrestrial and space climatology, but presents a formidable challenge. Sun and Earth are complex dynamic systems, which are linked through radiation, particles, and magnetic fields.

The open solar magnetic flux is one solar characteristic that is believed to have an influence Earth’s climate. A doubling of this flux during the 20th century has been inferred by Lockwood et al. [1999] and has been linked to a corresponding rise in Earth’s surface temperature during the last 100 years [Lockwood and Stamper, 1999]. Empirical models of the magnetic flux also show a large increase in the 20th century [Solanki, 2000].

These reports have engendered controversy, leading to a series of papers in the October 2002 issue of the Journal of Geophysical Research. In particular, there is no evidence for an increase in the solar flux after ~1955 [e.g., Arge et al., 2002, Richardson et al., 2002, Kotov and Kotova, 2001]. This absence of an increase in the recent data has raised questions about the reality of the reported increase prior to 1955. The doubt has been substantiated by one of us [8], who used polar cap geomagnetic fields to found no long-term trend in the solar wind electric field between 1926 and 2001.

The ensuing contradictions suggest that the aa index is not uniformly calibrated, since Lockwood et al. [1999] results are based on aa and their method is sound.

To exploit the long time-series of geomagnetic variations available, new indices are being proposed [7], that will separate the influence of solar wind speed and the interplanetary magnetic field.

References:

  • Arge, C. N., E. Hildner, V. J. Pizzo, and J. W. Harvey, Two solar cycles of non-increasing magnetic flux, J. Geophys. Res., 107(A10), 10.1029/2001JA000503, 1319, 2002
  • Kotov, V.A, I.V. Kotova, Does the Solar Magnetic Field Increase? Astron. Letters, 27, 260-266, 2001
  • Lockwood et al., A doubling of the Sun’s coronal magnetic field during the past 100 years, Nature, 399, 437-439, 1999
  • Solanki et al., Evolution of the Sun’s large-scale magnetic field since the Maunder Minimum, Nature, 408, 445-447, 2000
  • Richardson, I. G., E. W. Cliver, and H. V. Cane, Long-term trends in interplanetary magnetic field strength and solar wind structure during the twentieth century, J. Geophys. Res., 107(A10), 1304, doi:10.1029/2001JA000507, 2002
  • Willson, R. C., and A. V. Mordvinov, Secular total solar irradiance trend during solar cycles 21-23, Geophys. Res. Lett., 30, no. 5, 1199, doi:10.1029/2002GL016038, 2003

Transport of Energetic Particles into the Near-Earth Space Environment

The rate at which energetic particles and magnetic flux (flux tubes) are transported into the inner portion of Earth’s magnetosphere is a major factor affecting the ionosphere and the near-Earth radiation environment. Disturbances in the ionosphere can disrupt telecommunications, navigation, and GPS signals. The radiation environment poses a hazard to pilots, astronauts, and satellite systems. The critical quantity that determines flux-tube transport through Earth’s magnetosphere is its specific entropy. The specific entropy depends on the large-scale magnetic geometry which undergoes large variations, while only sparse point measurements of that geometry are available from a few satellites. In our research, we demonstrate a technique whereby the specific entropy can be estimated from measurements of the magnetic field and particle distribution at a single satellite. The results show that transport into the inner portion of Earth’s magnetosphere is dominated by flux tubes of low specific entropy (“bubbles”).
  • Bubble interchange appears to be the major form of transport in Earth’s magnetic tail, and geomagnetic conditions near Earth result from this transport.
  • Quantification of this transport is crucial for understanding, modeling, and eventual prediction of critical space-weather events.
  • One goal of this project is to provide quantitative observational information for use in specifying that transport and near-Earth geomagnetic conditions.

The solar wind flowing outward from the Sun interacts with Earth’s magnetic field to confine and compress the magnetic field on the day side and form a wake or tail downstream of Earth. This is Earth’s “magnetosphere”. The Earth’s magnetic field confines a plasma. The plasma is a completely ionized, electrically neutral, collisionless gas consisting of solar-wind protons, atmospheric oxygen ions, and electrons. The plasma behaves as an ideal gas with specific entropy, s = PV5/3, where P = nkT is the plasma pressure, and V is the flux-tube volume. The differential drifts between the plasma’s ions and electrons result in electrical currents which couple to Earth’s ionosphere. Normally, earthward transport in the magnetic tail is weak. However, during geomagnetic storms and substorms, magnetic reconnection occurs in the middle portion of the magnetic tail which substantially reduces the specific entropy of flux tubes. These flux tubes of reduced specific entropy, or “bubbles”, rapidly interchange with flux tubes of larger specific entropy. This results in the rapid transport of energetic plasma and magnetic flux toward Earth. These low-specific-entropy bubbles preferentially deposit their energetic plasma and magnetic flux near Earth and determine the electrical coupling of the magnetosphere with the Earth’s ionosphere.

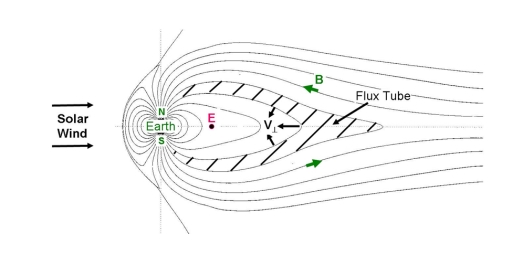
Hence, the specific entropy of flux tubes in Earth’s magnetic tail is a critical quantity that determines both geomagnetic conditions and the energetic particle environment near Earth. The problem is that determination of the specific entropy requires determination of the flux-tube volume, V. Whereas the plasma pressure is approximately constant within a flux tube (so a point measurement of the pressure suffices), the direct measurement of V is impossible. Space is large, spacecraft coverage is sparse, and the magnetic field varies greatly in both time and space. We have developed a method by which to estimate the volume of a flux tube given a point measurement of the magnetic field at a spacecraft [Wolf et al., 2006]. The method involves fitting a single, spacecraft measurement of the plasma pressure and magnetic field to a generalized solution for the global plasma and magnetic field configuration in force balance. The volume, of the flux tube sampled by the spacecraft is calculated from this fitted solution, and the specific entropy, s = PV5/3, of the sampled flux tube is estimated.

Here, as a typical example, we show one hour of measurements taken at the Geotail satellite on July 5, 1995 during a modest magnetospheric substorm. The first figure shows measurements of the magnetic field and its inclination. The second figure shows the plasma moments — three components of the bulk velocity, density, pressure, and the ratio of the plasma to magnetic pressures. The third panel shows quantities derived from the measurements. Of particular interest here is the first panel showing our estimate for the specific entropy of flux tubes as they move past the spacecraft and toward Earth. Notice that episodes of fast (hundreds of kilometers per second) earthward flow corresponds to times of reduced specific entropy PV5/3. Our method for estimating the instantaneous flux-tube volume given a point measurement of the magnetic field and plasma permits, for the first time, determination of the specific entropy in Earth’s magnetic tail. This quantity is critical in determining the energetic particle environment near Earth as well as the electrical coupling of Earth’s magnetosphere with its ionosphere and upper atmosphere.

We have introduced a method to obtain the specific entropy of flux tubes from single-satellite measurements of the plasma and magnetic field. We confirm that rapid Earthward transport of plasma and magnetic flux occurs as flux tubes of reduced specific entropy (“bubbles”). Quantitative determination of the specific entropy of flux tubes is critical for the understanding, modeling, and eventual prediction of space-weather events that affect power grids, communication, navigation, as well as radiation exposure to humans and satellite assets.

References:

Wolf, R. A., V. Kumar, F. R. Toffoletto, G. M. Erickson, A. M. Savoie, C. X. Chen, and C. L. Lemon (2006), Estimating local plasma sheet PV5/3 from single-spacecraft measurements, J. Geophys. Res., 111, A12218, doi:10.1029/2006JA012010

This project is supported by NASA under grant NNG06GH72G to Prairie View A&M University. Geotail magnetic field and plasma data were provided by T. Nagai, H. Hayakawa, and T. Mukai through DARTS at the Institute of Space and Astronautical Science (ISAS) in Japan.